Геодезический купол - это сферическое архитектурное сооружение, собранное из элементов, образующих геодезическую структуру, благодаря которой сооружение в целом обладает хорошими несущими качествами. Название это происходит от геодезических линий - линий наносимых на поверхность сферы, при помощи которых и строится купол. Геодезический купол является несущей сетчатой оболочкой. Форма купола образуется благодаря особому соединению балок в каждом узле сходятся ребра слегка различной длины, которые в целом образуют многогранник, близкий по форме к сегменту сферы. В основном, для проектирования купола используется экосаэдр - форма многогранника вписанного в сферу. Попробуем построить его в Inventor.
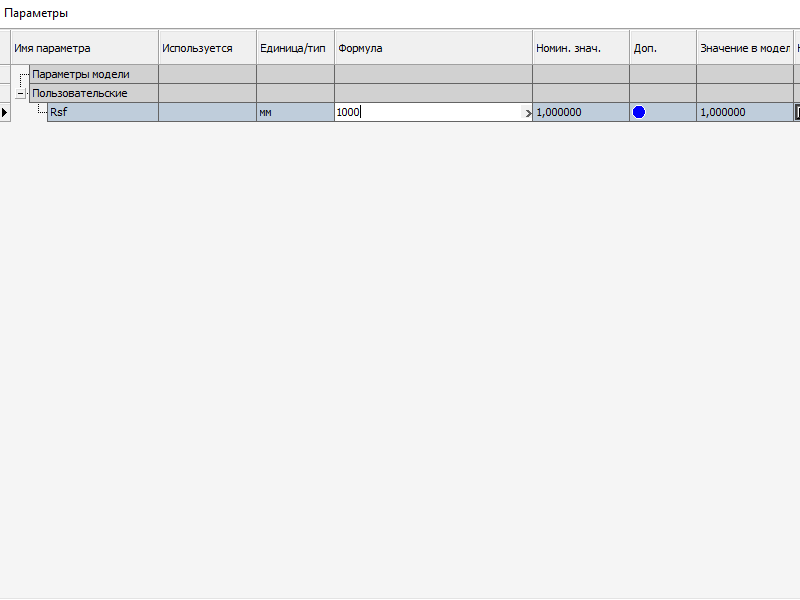
1.1 Создаем параметр Rsf = 1000мм , который равен радиусу нашей сферы.
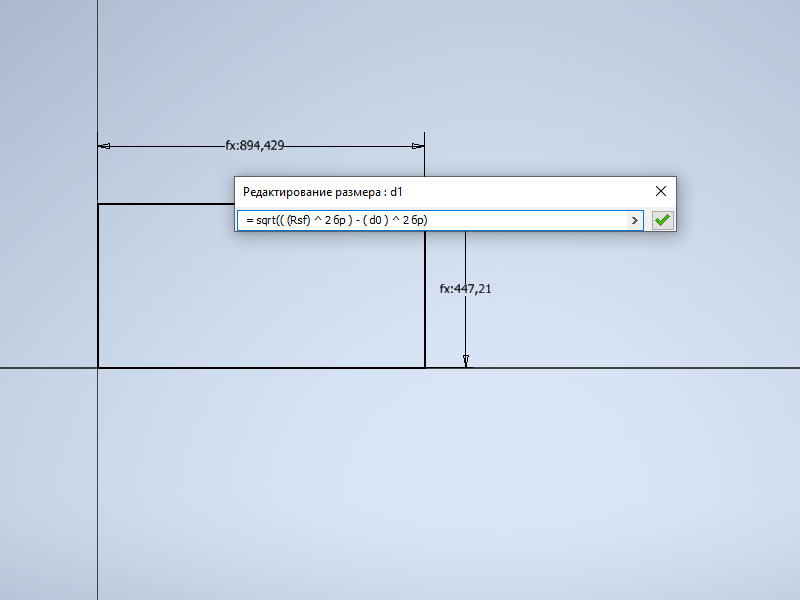
1.2 Строим прямоугольник с высотой равной Rsf*2/sqrt(5). Вторая сторона прямоугольника определяется по теореме Пифагора и равна (Rsf^2 - (Rsf*2/sqrt(5))^0.5
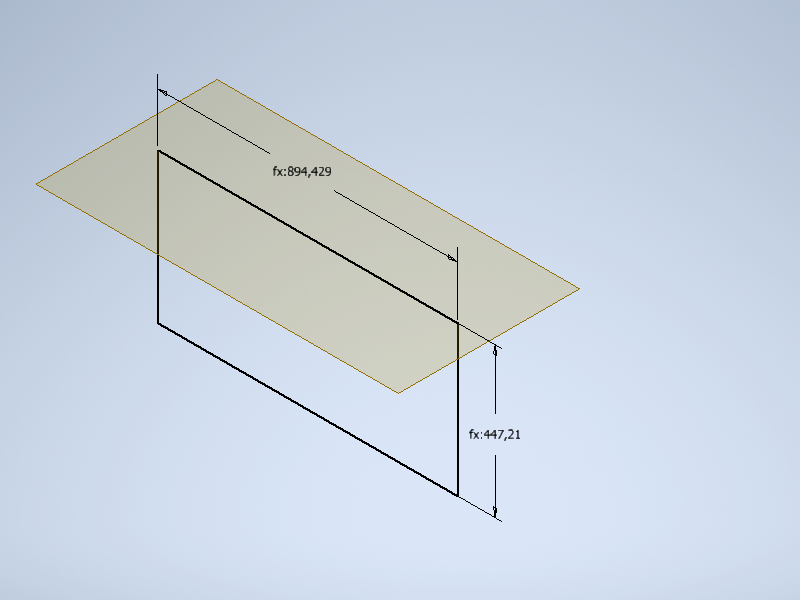
1.3 Строим рабочую плоскость параллельно плоскости X0Z через вершину четырехугольника
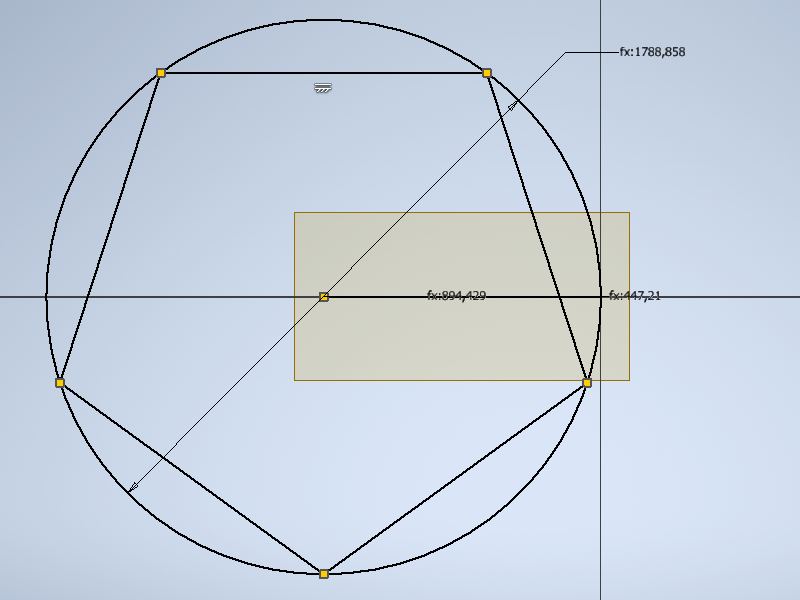
1.4 На построенной плоскости строим окружность диаметром равной двум большим сторонам четырехугольника и выписываем в нее правильный пятиугольник. Одну из сторон которого привязывем к оси Х зависимостью. на одной из сторон выносим размер (система посчитает его справочным - соглашаемся).
1.5 Выполняем операцию "выдавливание", переключаем режим с "твердое тело" на "поверхность" и строим цилиндр, основой которого будет окружность построенная в п 1.4.
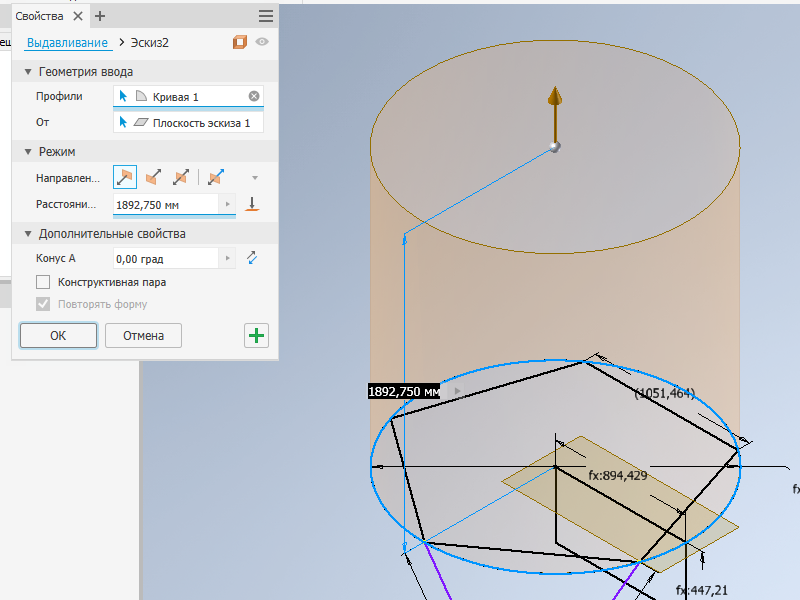
1.6 Включаем режим "построение 3d эскиза", строим два отрезка от двух вершин пятиугольника, сходящихся в одной точке. Длины отрезков ставим равные длинам сторон пятиугольника. Эта длина и будет длиной грани икосаэдра. Завершаем редактирование эскиза. Привязываем точку схождения отрезков зависимостью "совмещение" к поверхности цилиндра.
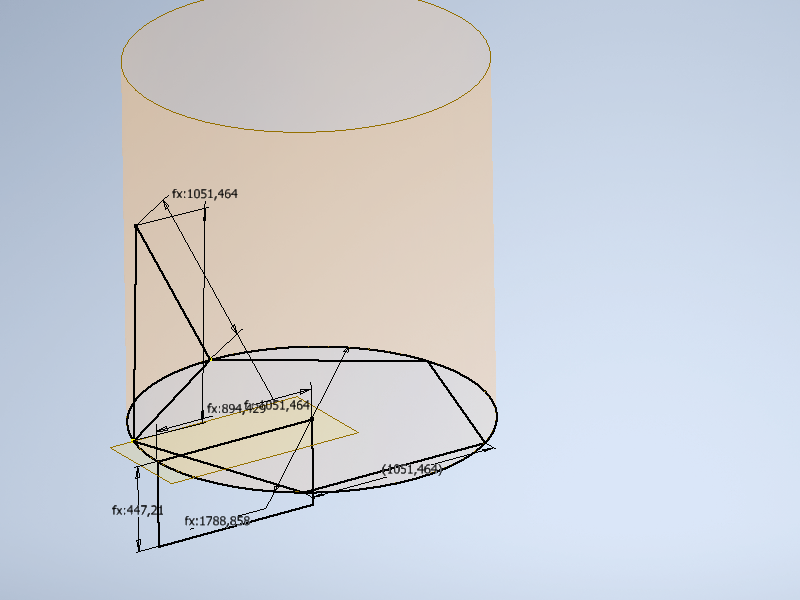
1.7 Строим еще одну рабочую плоскость параллельную Х0Z проходящую через точку схождения отрезков построенный в предыдущем пункте. Повторяем операции по построению окружности и пятиугольника п.1.4. пятиугольник при этом должен быть развернут относительно первого на 1/10 окружности. Отключаем видимость рабочих плоскостей, что бы не мешали дальнейшим построениям.
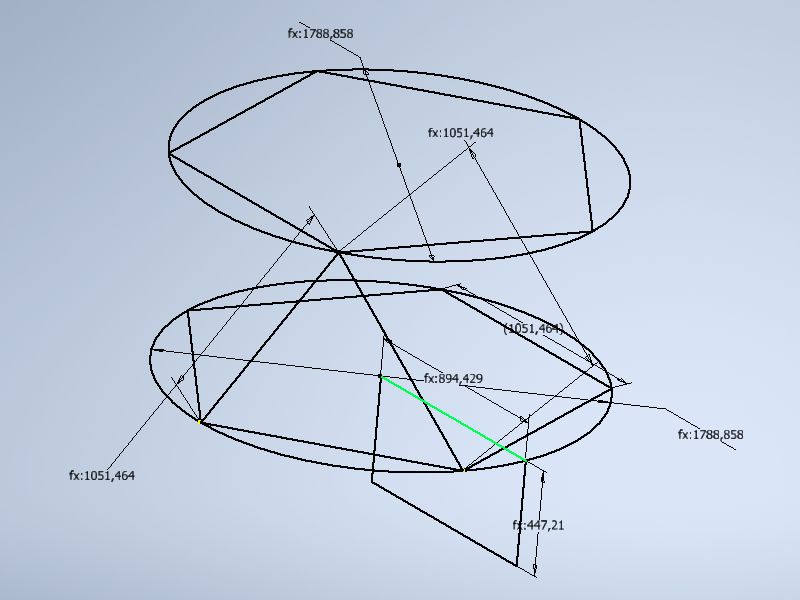
1.8 Зайдем в "Управление" - "Параметры" и проверим как реагирую наши построения на изменение радиуса сферы Rsf . Все должно пропорционально изменяться с изменением радиуса.
1.9 Заходим в редактирование 3d эскиза из п. 1.6 и строим отрезок вдоль оси Y проходящий через центр первого пятиугольника. Это необходимое построение для определения верхних и нижних частей икосаэдра. Включаем построение нового 3d эскиза, строим отрезок соединяющий два угла пятиугольника (строим вторую грань) и два отрезка соединенных в одной точке и исходящих из углов второго пятиугольника. Привязываем точку схождения отрезков к отрезку построенному вдоль оси Y зависимостью "совмещение". Длины отрезков должны быть равны длине стороны пятиугольника. Таким образом мы построили две боковые грани и одну верхнюю икосаэдра. На изображении ниже, я отключил отображение размеров что бы не захламлять рисунок.
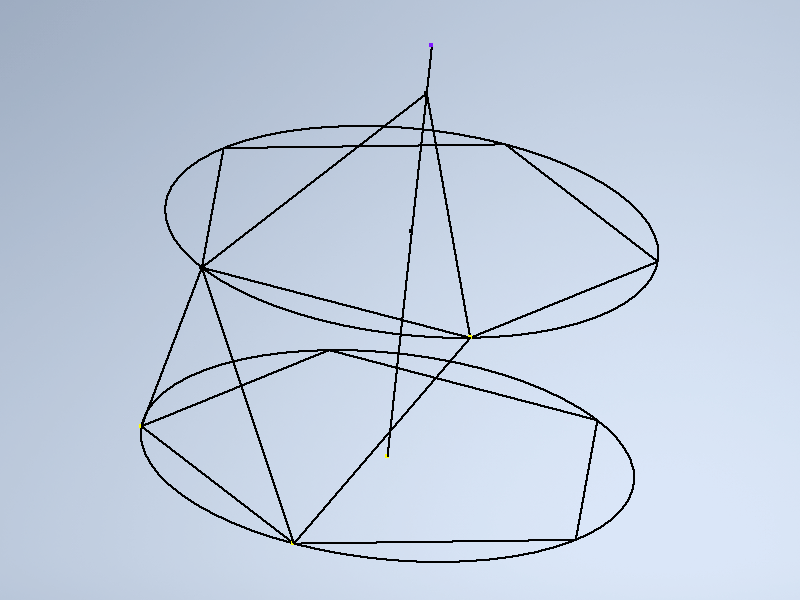
1.10 При необходимости можно достроить и нижнюю грань икосаэдра, но нам, для построения геодезического купола нужна только одна часть полусферы, поэтому перейдем дальше: В зависимости от задач поставленных в проекте, каждая грань икосаэдра может делиться на 2,3 и т.д. частей. Соответственно геодезический купол будет получать обозначение 2V, 3V и так далее. Принцип деления при этом остается одним и тем же. Я останавлюсь на 2V для сокращения построений и большей наглядности. Для построения такого купола необходимо разделить каждое из построенных ребер на 2 части, соответственно грань разделится на 4 тругольника. Итак, открываем новый 3d эскиз и делим три грани икосаэдра на 4 части каждую. Пробуем изменить размеры сферы в параметрах и убеждаемся, что чертеж так же меняется без ошибок.
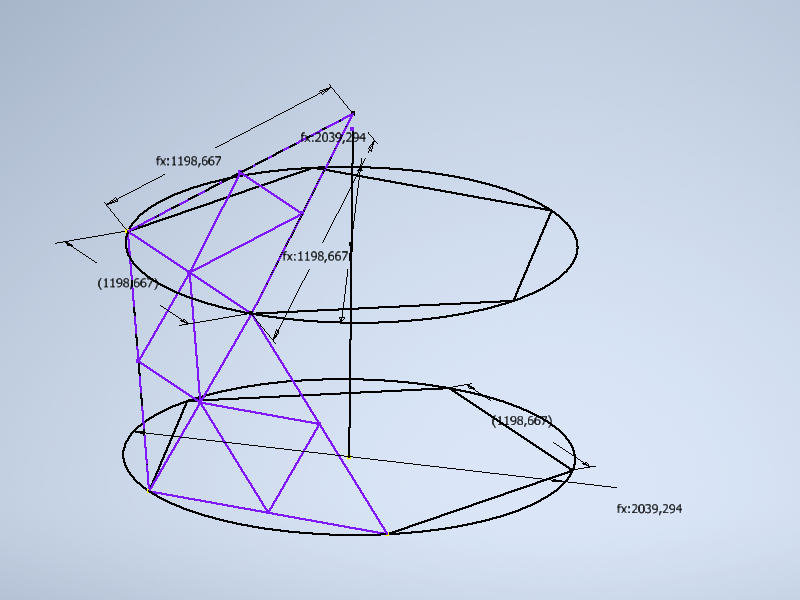
1.11 На данный момент мы построили три грани икосаэдра и разделили каждую на 4 части. Что бы построить годезический купол необходимо спроецировать построенные треугольники на поверхность сферы. Построим ее. НА плоскости X0Y от начала координат откладываем отрезок равный 2 * Rsf. перпендикулятно ему строим отрезок равный радиусу сферы. Далее строим дугу по трем точкам , которая будет являться образующей нашей сферы.
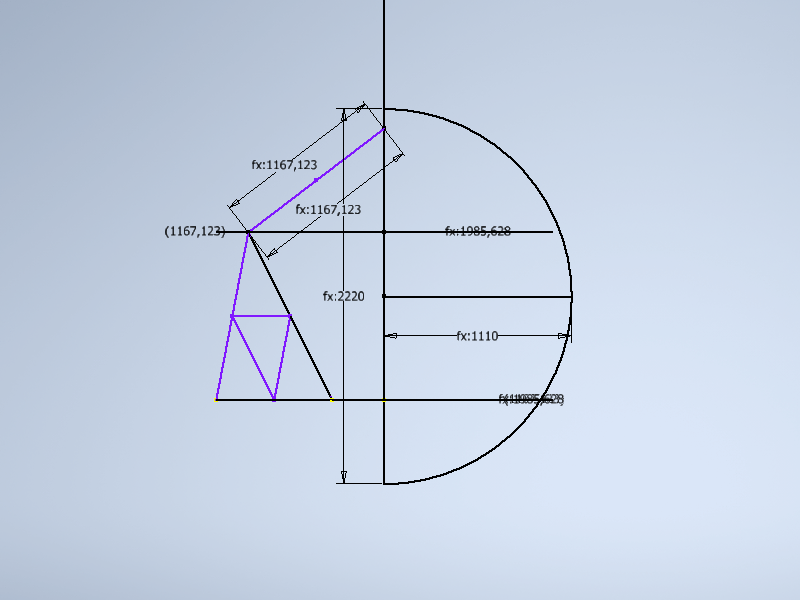
Выбираем операцию тело вращения с опцией грань, в качестве оси - ось XY. Отключаем все лишнее кроме эскиза с треугольниками и сферы.

1.12 Спроецируем разбитые грани икосаэдра на поверхность сферы. В качестве опции надо выбирать кратчайшее расстояние.
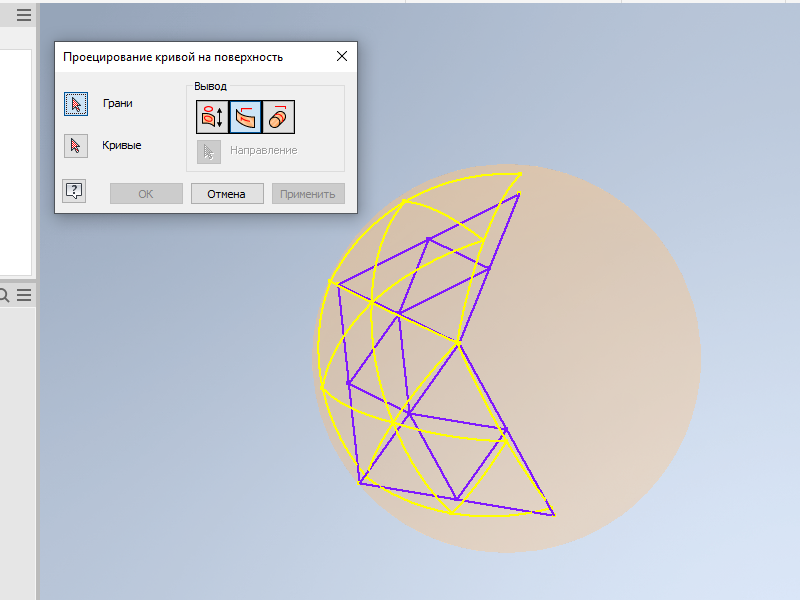
1.13 Соеденив узловые точки полученных дуг прямыми отрезками, мы получаем линии геодезического купола:
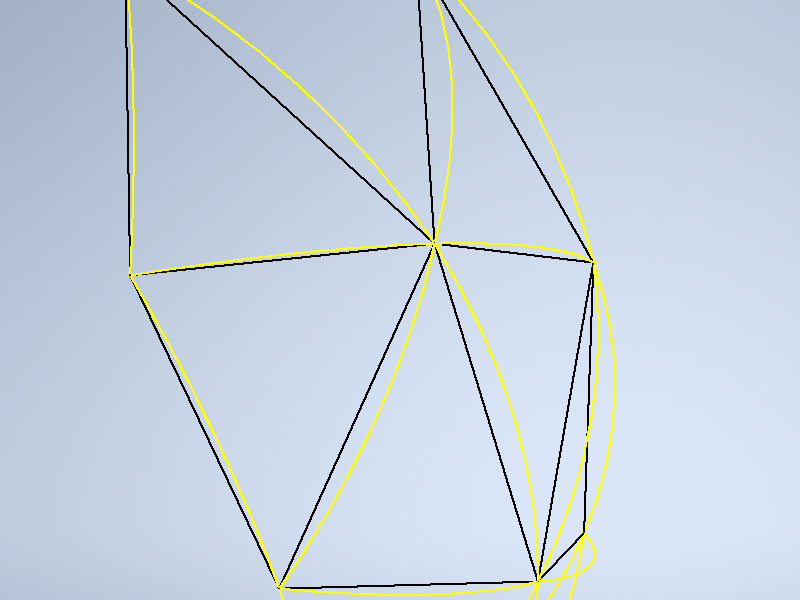
1.14 Что бы достроить купол полностью и не тратить время на построение отрезков, проецирование и т.д. выполним следующую операцию - построим части плоских поверхностей из получившихся линий купола и воспользуемся массивом поворота, с опциями "360 градусов" , "5 частей"
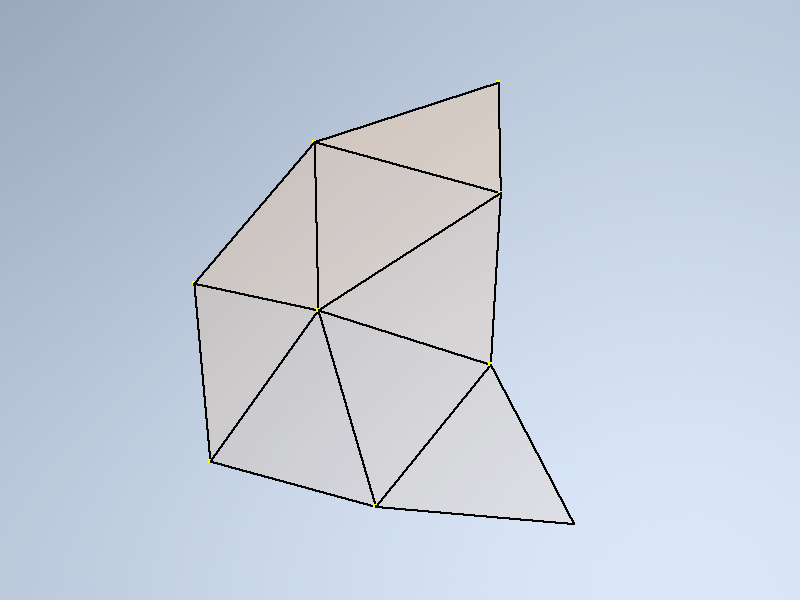

Как вы можете заметить, я оставил только три ряда граней, потому что они как раз образуют полусферу геодезического купола. После всех этих манипуляций, можно передать построенный каркас в сборку и , например, при помощи генератора рам разработать каркас будущего изделия.




